Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.3.5 Relations
3.3.5.1 Pairs and Cartesian product
|
|-> |
Pair |
|
** |
Cartesian product |
- Description
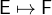 denotes the pair whose first element is
denotes the pair whose first element is 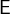 and second element is
and second element is 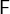 .
. 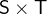 denotes the set of pairs where the first element is a member of
denotes the set of pairs where the first element is a member of 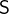 and second element is a member of
and second element is a member of 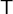 .
. - Definition
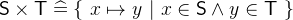
- Types
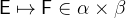 with
with 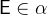 and
and 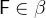 .
.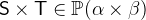 with
with 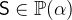 and
and 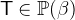 .
. - WD
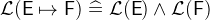
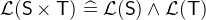
3.3.5.2 Relations
|
<-> |
Relations |
|
<<-> |
Total relations |
|
<->> |
Surjective relations |
|
<<->> |
Total surjective relations |
- Description
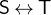 is the set of relations between the two sets
is the set of relations between the two sets 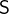 and
and 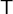 . A relation consists of pairs where the first element is of
. A relation consists of pairs where the first element is of 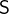 and the second of
and the second of 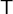 .
. 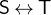 is just an abbreviation for
is just an abbreviation for 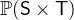 .
. A total relation is a relation which relates each element of
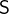 to at least one element of
to at least one element of 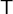 .
. A surjective relation is a relation where there is at least one element of
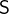 for each element of
for each element of 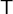 such that both are related.
such that both are related. - Definition
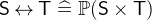
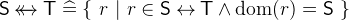
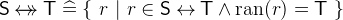
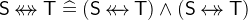
- Types
For
 and
and 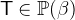 for each operator
for each operator  of
of 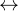 ,
, 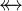 ,
, 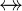 ,
, 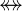 :
: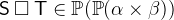
- WD
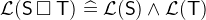 for each operator
for each operator  of
of 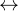 ,
, 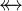 ,
, 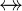 ,
, 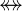 .
.
3.3.5.3 Domain and Range
|
dom |
Domain |
|
ran |
Range |
- Description
If
 is a relation between the sets
is a relation between the sets  and
and 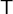 , the domain
, the domain 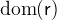 is the set of the elements of
is the set of the elements of 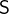 that are related to at least one element of
that are related to at least one element of  by
by  .
. Likewise the range
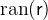 is the set of elements of
is the set of elements of  to which at least one element of
to which at least one element of  relates by
relates by  .
. - Definition
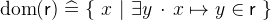
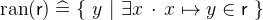
- Types
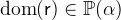 and
and 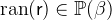 with
with 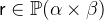 .
. - WD
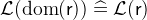
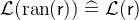
3.3.5.4 Domain and Range Restrictions
|
<| |
Domain restriction |
|
<<| |
Domain subtraction |
|
|> |
Range restriction |
|
|>> |
Range subtraction |
- Description
The domain restriction
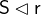 is a subset of the relation
is a subset of the relation  that contains all of the pairs whose first element is in
that contains all of the pairs whose first element is in 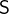 .
. 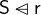 is the subset where the pair’s first element is not in
is the subset where the pair’s first element is not in 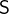 .
. In the same way, the range restriction
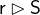 is a subset that contains all of the pairs whose second element is in
is a subset that contains all of the pairs whose second element is in 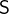 and
and 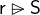 is the set where the pair’s second element is not in
is the set where the pair’s second element is not in 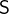 .
. - Definition
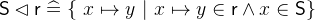
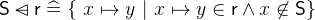
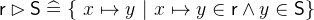
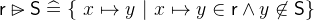
- Types
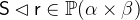 and
and 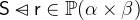 with
with 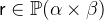 and
and 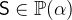
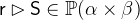 and
and 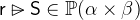 with
with 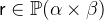 and
and 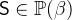
- WD
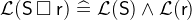 for each operator
for each operator  of
of  ,
, 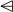 ,
, 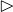 ,
, 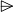
3.3.5.5 Operations on relations
|
; |
Relational forward composition |
|
circ |
Relational backward composition |
|
<+ |
Relational override |
|
|| |
Parallel product |
|
>< |
Direct product |
|
~ |
Inverse |
- Description
An element
 is related by
is related by 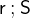 to an element
to an element 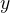 if there is an element
if there is an element  such that
such that  relates
relates  to
to  and
and 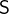 relates
relates  to
to 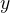 .
.  can be written as an alternative to
can be written as an alternative to 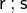 . This reflects the fact that
. This reflects the fact that 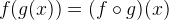 holds for two functions
holds for two functions 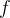 and
and 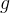 .
. The relational overwrite
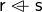 is equal to
is equal to  except all entries in
except all entries in  whose first element is in the domain of
whose first element is in the domain of  are replaced by the corresponding entries in
are replaced by the corresponding entries in  .
. The parallel product
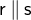 relates a pair
relates a pair  to a pair
to a pair  when
when  relates
relates  to
to 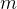 and
and  relates
relates 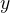 to
to 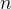 .
. If a relation
 relates an element
relates an element  to
to 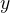 and
and  relates
relates  to
to  , the direct product
, the direct product 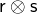 relates
relates  to the pair
to the pair  .
. The inverse relation
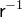 relates an element
relates an element  to
to 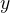 if the original relation
if the original relation  relates
relates 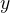 to
to  .
. - Definition
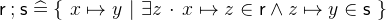

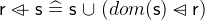
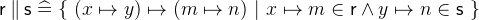
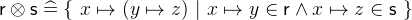
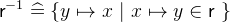
- Types
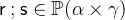 with
with 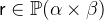 and
and 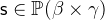
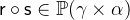 with
with 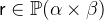 and
and 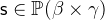
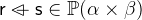 with
with 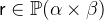 and
and 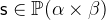
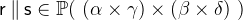 with
with 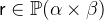 and
and 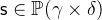
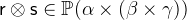 with
with 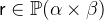 and
and 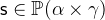
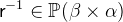 with
with 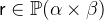
- WD
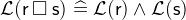 for each operator
for each operator  of
of  ,
,  ,
, 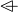 ,
,  ,
, 
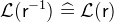
3.3.5.6 Relational image
|
[…] |
Relational image |
- Description
The relational image
![$\textsf{r}[\textsf{S}]$](images/img-0910.png) are those elements in the range of
are those elements in the range of  that are mapped from
that are mapped from  .
. - Definition
![$\textsf{r}[\textsf{S}] \mathrel {\widehat=}\{ ~ y~ |~ \exists x~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ x\in \textsf{S}\land x\mapsto y\in \textsf{r}~ \} $](images/img-0911.png)
- Types
![$\textsf{r}[\textsf{S}]\in \mathop {\mathbb P\hbox{}}\nolimits (\beta )$](images/img-0912.png) with
with 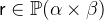 and
and 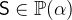
- WD
![$\mathcal{L}(\textsf{r}[\textsf{S}])\mathrel {\widehat=}\mathcal{L}(\textsf{r})\land \mathcal{L}(\textsf{S})$](images/img-0913.png)
3.3.5.7 Constant relations
|
id |
Identity relation |
|
prj1 |
First projection |
|
prj2 |
Second projection |
- Description
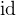 is the identity relation that maps every element to itself.
is the identity relation that maps every element to itself. 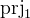 is a function that maps a pair to its first element. Likewise
is a function that maps a pair to its first element. Likewise 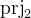 maps a pair to its second element.
maps a pair to its second element. 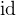 ,
, 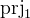 and
and 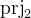 are generic definitions. Their type must be inferred from the environment.
are generic definitions. Their type must be inferred from the environment. - Definition
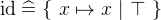
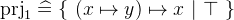
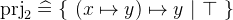
- Types
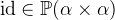 for an arbitrary type
for an arbitrary type 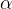 .
.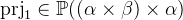 and
and 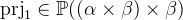 for arbitrary types
for arbitrary types 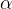 and
and 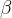 .
. - WD
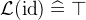
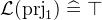
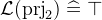
- Example
The assumption that a relation
 is irreflexive can be expressed by:
is irreflexive can be expressed by: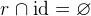
3.3.5.8 Sets of functions
|
+-> |
Partial functions |
|
–> |
Total functions |
|
>+> |
Partial injections |
|
>-> |
Total injections |
|
+->> |
Partial surjections |
|
–>> |
Total surjections |
|
>->> |
Bijections |
- Description
A partial function from
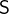 to
to 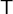 is a relation that maps an element of
is a relation that maps an element of 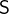 to at most one element of
to at most one element of 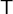 . A function is total if its domain contains all elements of
. A function is total if its domain contains all elements of 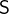 , i.e. it maps every element of
, i.e. it maps every element of 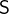 to an element of
to an element of 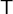 .
. A function is injective (is an injection) if two distinct elements of
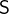 are always mapped to distinct elements of
are always mapped to distinct elements of 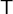 . It is also equivalent to say that the inverse of an injective function is a also a function.
. It is also equivalent to say that the inverse of an injective function is a also a function. A function is surjective (is a surjection) if for every element of
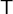 there exists an element in
there exists an element in 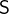 that is mapped to it.
that is mapped to it. A function is bijective (is a bijection) if it is both injective and surjective.
- Definition
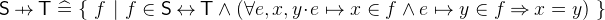
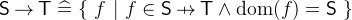
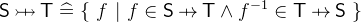
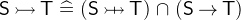
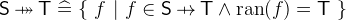
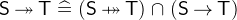
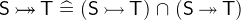
- Types
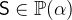 ,
, 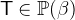 for each operator
for each operator  of
of 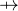 ,
, 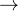 ,
,  ,
,  ,
, 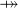 ,
,  ,
,  :
: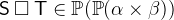
- WD
For each operator
 of
of 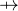 ,
, 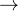 ,
,  ,
,  ,
, 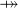 ,
,  ,
,  :
: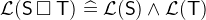
3.3.5.9 Function application
|
(…) |
Function application |
- Description
The function application
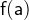 yields the value for
yields the value for  of the function
of the function 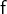 . It is only defined if
. It is only defined if  is in the domain of
is in the domain of 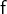 and if
and if 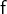 is actually a function.
is actually a function. - Definition
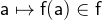
- Types
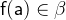 with
with 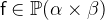 and
and 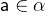
- WD
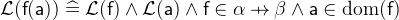 with
with 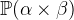 being the type of
being the type of 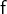 .
.
3.3.5.10 Lambda
|
% |
Lambda |
- Description
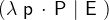 is a function that maps an “input”
is a function that maps an “input” 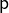 to a result
to a result 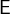 such that
such that 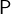 holds.
holds. 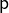 is a pattern of identifiers, parentheses and
is a pattern of identifiers, parentheses and  which follows the following rules:
which follows the following rules: An identifier
 is a pattern.
is a pattern. An identifier
 , followed by an
, followed by an 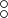 operator is a pattern (See 3.3.7 for more details).
operator is a pattern (See 3.3.7 for more details). A pair
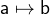 is a pattern if
is a pattern if  and
and 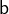 are patterns.
are patterns. 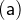 is pattern if
is pattern if  is pattern.
is pattern.
In the simplest case,
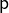 is just an identifier.
is just an identifier. - Definition

- Types
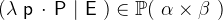 with
with 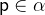 ,
, 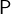 being a predicate and
being a predicate and 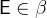 .
. - WD
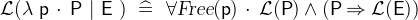
- Example
A function
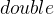 that returns the double value of a natural number:
that returns the double value of a natural number:
The dot product of two 2-dimensional vectors can be defined by:
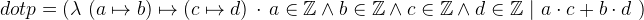
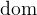
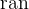
![$[\ldots ]$](images/img-0909.png)