Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.7.1 Contexts
A context has the following components:
- Sets
User-defined types can be declared in the SETS section (see Section 3.3.4 for more information).
- Constants
We can declare constants here. The type of each constant must be declared in the axiom section.
- Axioms
The axiom section contains a list of predicates (called axioms). These axioms define rules that will always be the case for given elements of the context. These rules can then be taken for granted when developing a model. The axioms can be used later in proofs that for components that use (“see”) this context. Each axiom has a label attached to it.
- Theorems
Axioms can be marked as theorems. If this is the case, we are declaring that the predicate can be proved by using the axioms that have been written before this theorem. Once they have been proven, theorems can be used later in proofs just like the other axioms.
- Extends
A context may extend an arbitrary number of other contexts. When we extend another context
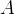 , we can then use all constants and axioms declared in
, we can then use all constants and axioms declared in 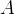 and also add new constants and axioms.
and also add new constants and axioms.
Rodin automatically generates proof obligations (often abbreviated as PO) for properties that need to be proven. Each proof obligation has a name that identifies where the proof obligation was generated. There are two kind of proof obligations generated in a context:
Each theorem must be proven. The proof obligation’s name has the form label/THM, where label is the theorem’s label.
Some expressions are not obviously well-defined. For example, the axiom
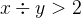 is only meaningful if
is only meaningful if 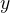 is different from 0. Thus Rodin generates the proof obligation
is different from 0. Thus Rodin generates the proof obligation 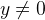 . A proof obligation for proving than an expression is well-defined has the name label/WD.
. A proof obligation for proving than an expression is well-defined has the name label/WD.
The order of the axioms and theorems matter because the proof of a theorem or the degree to which an expression is well-defined may depend on the axioms and theorems that have already been written. This is necessary to avoid circular reasoning.