Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.5.2 Data types
We have seen that each identifier (i.e. a variable, constant or parameter) must have a distinguished type. If we can introduce an identifier anywhere, we usually must also add a predicate with which the identifier’s type can be determined. In the traffic light example, a variable cars_go was introduced and the type was set by an invariant 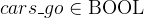 . In the next section, we’ll see that the type of constants is set by axioms (also predicates) and later we’ll see that the type for parameters will be determined by using guards (again, predicates).
. In the next section, we’ll see that the type of constants is set by axioms (also predicates) and later we’ll see that the type for parameters will be determined by using guards (again, predicates).
As a rule, each term in Event-B must have a certain type. When saving a Event-B component, Rodin starts the type checker to ensure that types are correctly used. For example, the terms on both sides of an equality ( ) must have the same type. If this is not the case, Rodin will generate an error message. For each type there exists a set that denotes exactly all elements that belong the type. We will now briefly give an overview about all types you might encounter.
) must have the same type. If this is not the case, Rodin will generate an error message. For each type there exists a set that denotes exactly all elements that belong the type. We will now briefly give an overview about all types you might encounter.
- Integers
We have already seen numbers, which are of type integer (
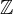 ). Example terms of type
). Example terms of type 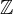 are
are 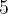 ,
, 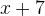 and
and 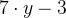 .
. - Booleans
We have already seen the Boolean type (
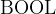 ) in the previous section (2.4). It has exactly two elements,
) in the previous section (2.4). It has exactly two elements, 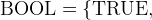
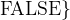 .
. - Carrier sets
A user can introduce a new type by adding its name to the Sets section of a context. We see that in more detail in the next section (2.6).
- Sets
If we have terms of a certain type, we can easily construct sets of that type. E.g.
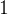 and
and 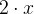 denote integers (
denote integers (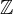 ) and
) and 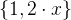 is a set of integers (
is a set of integers (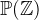 ).
). 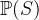 (ASCII: POW) denotes the power set (the set of all subsets) of
(ASCII: POW) denotes the power set (the set of all subsets) of 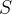 .
. - Pairs
If we have two terms, we can construct a pair. For example, with
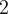 and
and 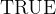 , we can construct the pair
, we can construct the pair 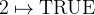 (ASCII: 2|->TRUE). The type of that pair is
(ASCII: 2|->TRUE). The type of that pair is 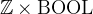 , where
, where 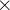 denotes the Cartesian product. Set of pairs (“relations”) play an important role in modelling languages like Event-B.
denotes the Cartesian product. Set of pairs (“relations”) play an important role in modelling languages like Event-B.
![\includegraphics[width=7mm]{img/warning_64.png}](images/img-0004.png)
Please do not confuse predicates and Boolean values! For example, if you want to express the condition “if the variable
is true,
should be greater than 2”, you cannot write
(That would produce a syntax error). Instead you have to write
.
In Section 3.3 the types of each operator in Event-B are described in detail.