Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.2.3 Contexts
A context describes the static part of a model. It consists of
Carrier sets
Constants
Axioms
Extended contexts
3.2.3.1 Carrier Sets
A new data type can be declared by adding its name – an identifier – to the Sets section. The identifier must be unique, i.e. it must not have been already declared as a constant or set in the current context or an extended context. The identifier is then implicitly introduced as a new constant (see below) that represents the set of all elements of the type.
A common pattern for declaring enumerated sets (sets where all elements are explicitly given) is to use the partition operator. If we want to specify a set 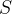 with elements
with elements  , we declare
, we declare 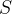 as a set,
as a set,  as constants and add the axiom
as constants and add the axiom 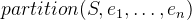 .
.
3.2.3.2 Extending a context
Other contexts can be extended by adding their name to the Extends section.
The resulting context consists of all constants and axioms of all extended contexts and the extending context itself. Thus for a context or machine that extends or sees the contexts, it makes no difference where a constant or axiom is declared.
Extending two contexts which declare a constant or set using the same identifier will result in an error.
3.2.3.3 Constants and axioms
Constants can be declared by adding their unique name (an identifier) to the Constants section. An axiom must also be in place from which the type of the constant can be inferred. We denote the sequence of all constants with 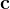 .
.
An axiom is a statement that is assumed to be true in the rest of the model. Each axiom consists of a label and a predicate 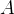 . All free identifiers in
. All free identifiers in 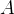 must be constants.
must be constants.
Axioms can be marked as theorems. The proof obligation that are then generated are described in Section 3.2.6.1. The validity of a theorem can be proven from the axioms that have already been declared.
The well-definedness of axioms must be proven if an axiom contains a well-definedness condition (3.2.5.1).