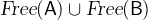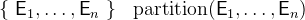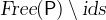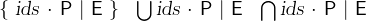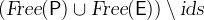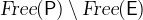Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.3.1 Introduction
In the following section, we use sans serif letters like  ,
, 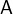 ,
, 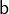 ,
, 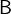 , …as placeholders for arbitrary expressions instead of
, …as placeholders for arbitrary expressions instead of 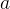 ,
, 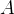 ,
, 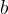 ,
, 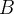 which represent Event-B identifiers. For example, the
which represent Event-B identifiers. For example, the  and
and 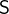 in
in 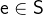 could be a placeholder for
could be a placeholder for 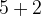 and
and 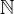 .
.
We use the  to state that an expression, predicate or assignment
to state that an expression, predicate or assignment 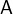 can be equivalently rewritten as
can be equivalently rewritten as 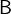 if
if 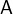 ’s well-definedness condition is fulfilled. We have tried to find a balance between having a precise and concise description for all Event-B’s mathematical components and having a text that is still easily readable. Many of the operators can be expressed using other, simpler constructs. Other, like equality (
’s well-definedness condition is fulfilled. We have tried to find a balance between having a precise and concise description for all Event-B’s mathematical components and having a text that is still easily readable. Many of the operators can be expressed using other, simpler constructs. Other, like equality ( ) or universal quantification (
) or universal quantification (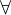 ) are simply described with natural language.
) are simply described with natural language.
When we introduce new identifiers while expressing an operator (e.g. by using a set comprehension), we assume that the new identifier does not occur free in the rewritten expressions (see Section 3.3.1.3 for more information on free identifiers).
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
For a concise summary of the Event-B mathematical toolkit, download the four-page Event-B Cheat Sheet. We would like to thank Ken Robinson for making it available.
3.3.1.1 Data types
In Event-B we have 3 kinds of basic data types:
Users can define carrier sets. These are defined in the Sets section of a context. Carrier sets are never empty. There is no other assumption made about carrier sets unless it is stated explicitly as an axiom.
From all data types 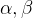 , two other kinds of data types can be constructed:
, two other kinds of data types can be constructed:
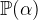 contains the sets of elements of
contains the sets of elements of 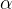 .
. 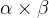 is the set of pairs where the first element is of type
is the set of pairs where the first element is of type 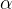 and the second element is of type
and the second element is of type 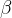 .
.
Expressions that are constructed by the rules above are called type expressions.
3.3.1.1.1 A note about the notation
We use the Greek letters 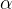 ,
, 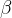 ,
, 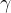 , …to represent arbitrary data types. For an expression
, …to represent arbitrary data types. For an expression 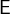 , we write
, we write 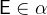 to state that
to state that 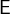 is of type
is of type 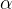 . In the following descriptions of Event-B’s mathematical constructs, we will describe the types of all constructs and their components.
. In the following descriptions of Event-B’s mathematical constructs, we will describe the types of all constructs and their components.
For example, we will describe the maplet  whose type is defined by
whose type is defined by 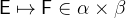 with
with 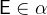 and
and 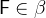 . We do not restrict the types of
. We do not restrict the types of 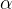 and
and 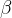 .
.
For predicates, we simply describe the data types of their components. The predicate itself does not have a type. For example, consider the components’ types for the equality of two expressions 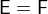 :
: 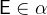 and
and 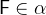 . By stating that
. By stating that 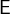 and
and 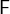 are both of type
are both of type 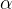 , we express that both expressions must have the same type but do not make any further assumptions about their types.
, we express that both expressions must have the same type but do not make any further assumptions about their types.
3.3.1.2 Well-definedness
A predicate which describes the condition under which an expression or predicate in Event-B can be safely evaluated is the well-definedness condition. An example with integer division makes this clear: The expression 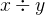 only makes sense when
only makes sense when 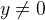 .
.
Well-definedness conditions are usually used for well-definedness proof obligations (3.2.5).
In Rodin, the 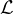 -operator defines which well-defined condition a predicate or expression has. When applied to the above example, integer division can be formatted as follows:
-operator defines which well-defined condition a predicate or expression has. When applied to the above example, integer division can be formatted as follows: 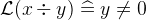 .
.
In the following sections, we state for each mathematical construct what the well-definedness conditions are. In many cases, this is just the conjunction of the well-definedness conditions for the different syntactical parts of a construct.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
The
-operator cannot be expressed in Event-B itself. It is only used to describe Event-B’s concept of well-definedness and how the well-definedness proof obligations are generated.
3.3.1.3 Free identifiers
Free identifiers in predicates and expressions are those identifiers which are used but not introduced by quantifiers. More formally, we define the set of free identifiers 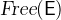 of an expression or predicate
of an expression or predicate 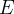 recursively as follows:
recursively as follows:
Expression / Predicate |
Free identifiers |
Identifier |
|
Integer |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3.1.4 Structure of the subsections
The following reference subsections will have the form the form:
math. Symbol |
ASCII representation |
Name of the operator |
… |
… |
… |
- Description
A short description of what the operator does
- Definition
A formal definition of what the operator does
- Types
A description of the types of all arguments and, if the operation is an expression, the expression’s type
- WD
A description of the well-definedness conditions using the
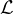 operator
operator - Feasibility
Non-deterministic assignments may have feasibility conditions. These are used in the proof obligations of an event (3.2.4.4.6).
- Example
For some constructs, an example is provided to clarify their use.
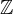 is the set of all integers.
is the set of all integers. 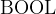 is the set of Booleans. It has two elements
is the set of Booleans. It has two elements 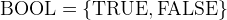 .
. 
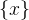
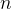
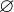
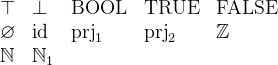

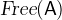
![$\begin{array}{lllll} \textsf{A}\land \textsf{B}& \textsf{A}\lor \textsf{B}& \textsf{A}\mathbin \Rightarrow \textsf{B}& \textsf{A}\mathbin \Leftrightarrow \textsf{B}& \textsf{A}=\textsf{B}\\ \textsf{A}\neq \textsf{B}& \textsf{A}\in \textsf{B}& \textsf{A}\not\in \textsf{B}& \textsf{A}\subseteq \textsf{B}& \textsf{A}\not\subseteq \textsf{B}\\ \textsf{A}\subset \textsf{B}& \textsf{A}\not\subset \textsf{B}& \textsf{A}\mathbin {\mkern 1mu\cup \mkern 1mu}\textsf{B}& \textsf{A}\mathbin {\mkern 1mu\cap \mkern 1mu}\textsf{B}& \textsf{A}\setminus \textsf{B}\\ \textsf{A}\mathbin \times \textsf{B}& \textsf{A}\mathbin \leftrightarrow \textsf{B}& \textsf{A}\mathbin {\leftarrow \mkern -14mu\leftrightarrow }\textsf{B}& \textsf{A}\mathbin {\leftrightarrow \mkern -14mu\rightarrow }\textsf{B}& \textsf{A}\mathbin {\leftrightarrow \mkern -14mu\leftrightarrow }\textsf{B}\\ \textsf{A}\mathbin \lhd \textsf{B}& \textsf{A}\mathbin {\lhd \mkern -14mu-}\textsf{B}& \textsf{A}\mathbin \rhd \textsf{B}& \textsf{A}\mathbin {\rhd \mkern -14mu-}\textsf{B}& \textsf{A}\mathbin ;\textsf{B}\\ \textsf{A}\circ \textsf{B}& \textsf{A}\mathbin {\lhd \mkern -9mu-}\textsf{B}& \textsf{A}\mathbin \| \textsf{B}& \textsf{A}\mathbin \otimes \textsf{B}& \textsf{A}[\textsf{B}] \\ \textsf{A} \mathbin {\mkern 6mu\mapstochar \mkern -6mu\rightarrow } \textsf{B}& \textsf{A}\mathbin \rightarrow \textsf{B}& \textsf{A} \mathbin {\mkern 9mu\mapstochar \mkern -9mu\rightarrowtail } \textsf{B}& \textsf{A}\mathbin \rightarrowtail \textsf{B}& \textsf{A} \mathbin {\mkern 6mu\mapstochar \mkern -6mu\twoheadrightarrow } \textsf{B}\\ \textsf{A}\mathbin \twoheadrightarrow \textsf{B}& \textsf{A}\mathbin { \rightarrowtail \mkern -18mu\twoheadrightarrow } \textsf{B}& \textsf{A}(\textsf{B}) & \textsf{A}+\textsf{B}& \textsf{A}-\textsf{B}\\ \textsf{A}\cdot \textsf{B}& \textsf{A}\div \textsf{B}& \textsf{A}\bmod \textsf{B}& \textsf{A}\mathbin {\widehat{\enskip }}\textsf{B}& \textsf{A}\mathbin {\raisebox{0.6ex}{\ensuremath{\circ }}\mkern -9mu\raisebox{-0.6ex}{\ensuremath{\circ }}}\textsf{B}\end{array}$](images/img-0649.png)