Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.4.2 Proof Rules
In its pure mathematical form, a proof rule is a tool to perform a formal proof and is denoted by:
![\[ \frac{\quad A\quad }{C} \]](images/img-1048.png) |
where 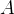 is a (possibly empty) list of sequents (the antecedents of the proof rule) and
is a (possibly empty) list of sequents (the antecedents of the proof rule) and  is a sequent (the consequent of the rule). We interpret the above proof rule as follows: The combination of the proofs of each sequent of
is a sequent (the consequent of the rule). We interpret the above proof rule as follows: The combination of the proofs of each sequent of 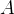 prove the sequent
prove the sequent  .
.
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
Example: Consider the following proof rule:
This says that if
is valid, then the statement
must be valid as well. Thus, we can replace the sequent by the consequent.
3.4.2.1 Proof Rule Representation in Rodin
In Rodin, the representation for proof rules is more structured not only to reduce the space required to store the rule but, more importantly, to support proof reuse. A proof rule in Rodin contains the following:
- used goal
A used goal predicate.
- used hypotheses
The set of used hypotheses.
- antecedents
A list of antecedents (to be explained later).
- reasoner
The reasoner used to generate this proof rule (see Section 3.4.6).
- reasoner input
The input for the reasoner to generate this proof rule (reasoners are explained in Section 3.4.6).
Each antecedent of the proof rule contains the following information:
- new goal
A new goal predicate.
- added hypotheses
The set of added hypotheses.
With this representation, a proof rule in Rodin corresponding to a proof schema as follows:
![\[ \begin{array}{c} H, H_ u, H_{A_0} \vdash G_{A_0} ~ ~ ~ \ldots ~ ~ ~ H, H_ u, H_{A_ n-1} \vdash G_{A_ n-1} \\ \hline H, H_ u \vdash G_ u \end{array} \]](images/img-1052.png) |
Where:
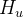 is the set of used hypotheses
is the set of used hypotheses 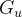 is the used goal
is the used goal 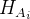 is the set of added hypotheses corresponding to the ith antecedent.
is the set of added hypotheses corresponding to the ith antecedent. 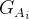 is the new goal corresponding to the ith antecedent.
is the new goal corresponding to the ith antecedent. 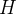 is the meta-variable that can be instantiated.
is the meta-variable that can be instantiated.
3.4.2.2 Applying Proof Rules
Given a proof rule of the form mentioned above, the following describes how to apply this rule to an input sequent. If the process is successful, a list of output sequences is produced.
The rule is not applicable if the goal of the sequent is not exactly the same as the used goal or if any of the used hypotheses are not contained in the set of hypotheses of the input sequent.
If the rule is applicable, the antecedent sequents are returned. The goal of each antecedent sequent is the new goal. The hypotheses of each antecedent sequent are the union of the old hypotheses and added hypotheses of the corresponding antecedent.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
The user interface for proving is explained in Section 3.1.7. The practical application of proof rules is explained in Section 2.9.6.
![\[ \frac{ E_1 }{ E_1 \lor E_2 } \]](images/img-1050.png)