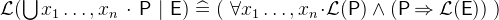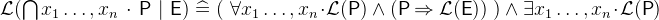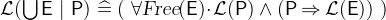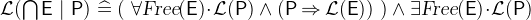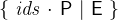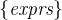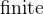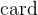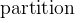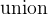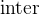Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.3.4 Sets
3.3.4.1 Set comprehensions
|
{ids.P|E} |
Set comprehension |
|
{E|P} |
Set comprehension (short form) |
- Description
ids is a comma-separated list of one ore more identifiers whose type must be inferable by the predicate
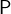 . The predicate
. The predicate 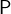 and
and 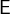 can contain references to the identifiers ids.
can contain references to the identifiers ids. The set comprehension
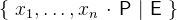 contains all values of
contains all values of 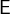 for the values of
for the values of  where
where 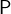 is true.
is true. 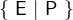 is a short form for
is a short form for 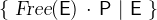 where
where 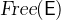 denotes the list of free identifiers occurring in
denotes the list of free identifiers occurring in 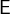 (see Section 3.3.1.3)).
(see Section 3.3.1.3)). - Definition
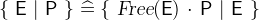
- Types
With
 and
and 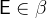 :
: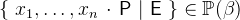
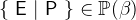
- WD
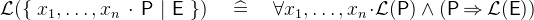
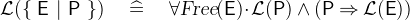
- Example
The following set comprehensions contain all the first 10 squares numbers:
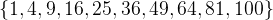
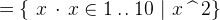

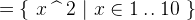
3.3.4.2 Basic sets
|
{} |
Empty set |
|
{exprs} |
Set extension |
- Description
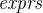 is a comma-separated list of one or more expressions of the same type.
is a comma-separated list of one or more expressions of the same type. The empty set
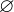 contains no elements. The set extension
contains no elements. The set extension  is the set that contains exactly the elements
is the set that contains exactly the elements  .
. - Definition
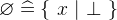
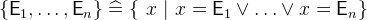
- Types
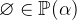 , where
, where 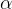 is an arbitrary type.
is an arbitrary type.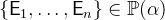 with
with 
- WD
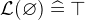
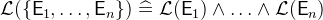
3.3.4.3 Subsets
|
<: |
subset |
|
/<: |
not a subset |
|
<<: |
strict subset |
|
/<<: |
not a strict subset |
- Description
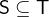 checks if
checks if 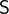 is a subset of
is a subset of 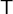 , i.e. if all elements of
, i.e. if all elements of 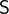 occur in
occur in 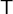 .
. 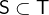 checks if
checks if 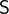 is a subset of
is a subset of 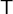 and
and 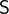 does not equal
does not equal 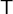 .
. 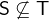 and
and 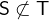 are the respective negated variants.
are the respective negated variants. - Definition
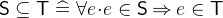
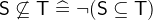
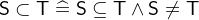
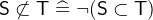
- Types
 is a predicate with
is a predicate with 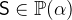 ,
, 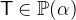 for each operator
for each operator  of
of  ,
, 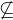 ,
,  ,
, 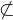 .
. - WD
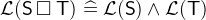 for each operator
for each operator  of
of  ,
, 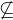 ,
,  ,
, 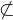 .
.
3.3.4.4 Operations on sets
|
\/ |
Union |
|
/\ |
Intersection |
|
\ |
Set subtraction |
- Description
The union
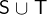 denotes the set that contains all elements that are in
denotes the set that contains all elements that are in 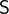 or
or 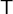 . The intersection
. The intersection  denotes the set that contains all elements that are in both
denotes the set that contains all elements that are in both 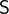 and
and 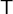 . The set subtraction or set difference
. The set subtraction or set difference 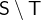 denotes all elements that are in
denotes all elements that are in 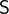 but not in
but not in 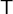 .
. - Definition
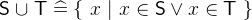
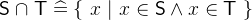
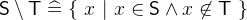
- Types
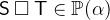 with
with 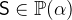 and
and 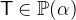 for each operator
for each operator  of
of  ,
,  ,
, 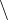
- WD
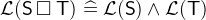 for each operator
for each operator  of
of  ,
,  ,
, 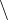
3.3.4.5 Power sets
|
POW |
Power set |
|
POW1 |
Set of non-empty subsets |
- Description
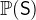 denotes the set of all subsets of the set
denotes the set of all subsets of the set 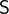 .
. 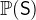 denotes the set of all non-empty subsets of the set
denotes the set of all non-empty subsets of the set 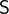 .
. - Definition
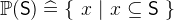
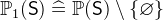
- Types
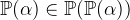 and
and 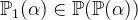 with
with 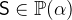 .
. - WD
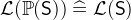
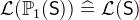
3.3.4.6 Finite sets
|
finite |
Finite set |
|
card |
Cardinality of a finite set |
- Description
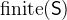 is a predicate that states that
is a predicate that states that 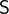 is a finite set.
is a finite set. 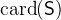 denotes the cardinality of
denotes the cardinality of 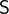 . The cardinality is only defined for finite sets.
. The cardinality is only defined for finite sets. - Definition
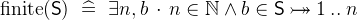
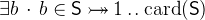
- Types
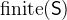 is a predicate and
is a predicate and 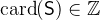 with
with 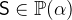 , i.e.
, i.e. 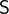 must be a set.
must be a set. - WD
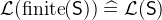
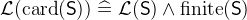
3.3.4.7 Partition
|
partition |
Partitions of a set |
- Description
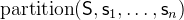 is a predicate that states that the sets
is a predicate that states that the sets  constitute a partition of
constitute a partition of 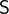 . The union of all elements of a partition is
. The union of all elements of a partition is 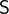 and all elements are disjoint.
and all elements are disjoint. 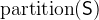 is equivalent to
is equivalent to 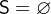 and
and 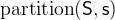 to
to 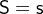 .
. - Definition
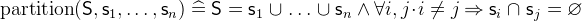
- Types
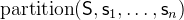 is a predicate with
is a predicate with 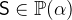 and
and 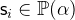 for
for 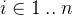
- WD

3.3.4.8 Generalized union and intersection
|
union |
Generalized union |
|
inter |
Generalized intersection |
- Description
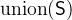 is the union of all elements of
is the union of all elements of 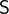 .
. 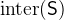 is the intersection of all elements of
is the intersection of all elements of 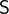 . The intersection is only defined for non-empty
. The intersection is only defined for non-empty 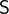 .
. - Definition
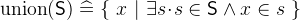
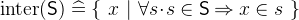
- Types
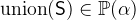 and
and 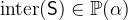 with
with 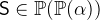 .
. - WD
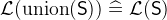
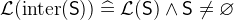
3.3.4.9 Quantified union and intersection
|
UNION |
Quantified union |
|
INTER |
Quantified intersection |
- Description
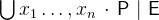 is the union of all values of
is the union of all values of 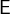 for valuations of the identifiers
for valuations of the identifiers  that fulfill the predicate
that fulfill the predicate 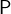 . The types of
. The types of  must be inferable by
must be inferable by 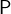 .
. Analogously is
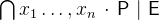 the intersection of all values of
the intersection of all values of 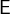 for valuations of the identifiers
for valuations of the identifiers  that fulfill the predicate
that fulfill the predicate 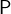 .
. Like set comprehensions (3.3.4.1), the quantified union and intersection have a short form where the free variables of the expression are quantified implicitly:
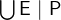 and
and 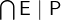 .
. - Definition
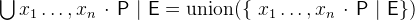
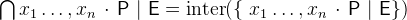
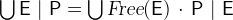
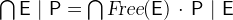
- Types
With
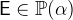 and
and 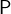 being a predicate:
being a predicate: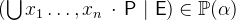
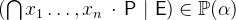
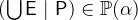
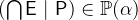
- WD