Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.5.6 Arithmetic
We have the usual operations on integers,  ,
,  ,
,  and
and 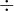 (ASCII: +, -, * and /). They can be compared with the usual equality operators:
(ASCII: +, -, * and /). They can be compared with the usual equality operators: 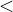 ,
, 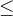 ,
, 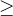 ,
, 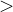 (ASCII: <, <=, >=, >).
(ASCII: <, <=, >=, >).
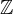 (ASCII: INT) denotes the set of all integer numbers.
(ASCII: INT) denotes the set of all integer numbers. 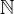 and
and 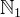 (ASCII: NAT and NAT1 respectively) are the subsets of natural numbers.
(ASCII: NAT and NAT1 respectively) are the subsets of natural numbers.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
If you specify two variables
and
with
and
, then both are of type integer (
).
is not another type. There is just the additional condition
.