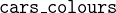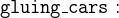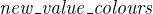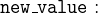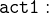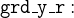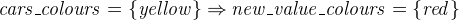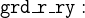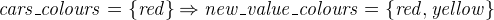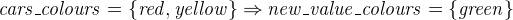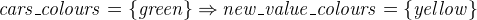Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.8.5 Witnesses
The refinement of set_cars is more difficult since the event uses a parameter (the new value for cars_go). In order to refine it, we need a witness (3.2.4.4.4).
A witness is to an event’s parameter what a gluing invariant is to a variable: it is a mapping between the abstract parameter and the new parameter and allows the abstract parameter to disappear. In this example, the abstract parameter new_value is of type BOOL, and we introduce a new parameter new_value_colours of type COLOURS.
![\includegraphics[width=7mm]{img/warning_64.png}](images/img-0004.png)
The naming of a witnesses’ label is extremely important. It must be the name of the abstract parameter. In our example, the label must be new_value
Let’s get started. We first provide the new variable, gluing invariant, typing invariant and initialisation as we have done before (at this point you can also rename the gluing invariant from the last section as gluing_peds in order to be able to determine between the two gluing invariants). Note that the traffic light for the cars can show more than one colour at a time. Therefore, the variable contains a set of colours instead of just one colour (as modelled for peds_colour):
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- VARIABLES
- INVARIANTS
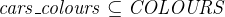
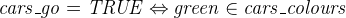
- EVENTS
- Initialisation
- begin
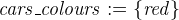
- end
- END
We also have to modify the guard on set_peds_green, which is something that you should now be able to figure out yourself (just replace cars_go = FALSE with green 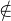 cars_colours).
cars_colours).
The interesting piece is the last event, set_cars, which we rename as set_cars_colours. We change the parameter to new_value_colours and type it as a subset of COLOURS.
The witness appears in the with section of the event. The label must be new_value. The value itself must describe the relationship between the abstract parameter new_value and the new parameter new_value_colours. As we use the parameter as the new value for the variable cars_colours, the witness is an adaptation of the gluing invariant (we just replace cars_colours with new_value_colours).
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
In most cases, the witness is a slightly modified gluing invariant.
Here is the resulting event:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- Event
set_cars_colours

- refines
set_cars
- any
- where
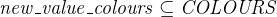
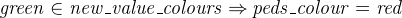
- with
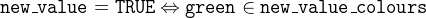
- then
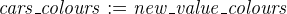
- end
Now you can get rid of the variable cars_go and its initialisation clause, and there will not be any errors or warnings. But even though all proof obligations are now discharged, we’re not done yet. Even though the traffic light doesn’t violate the safety property from the abstract machine, it doesn’t behave the way described in Section 2.8.1. We still have to ensure that the lights are activated in the proper sequence. We can impose this behavior by adding four guards each of which define one transition: