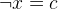Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.9.6 The First Proof
In this section, we will carry out proofs for the model of the Celebrity Problem. To do this, click on the box in the upper right hand corner that has a little plus sign and switch to the Proving Perspective. You can switch between perspectives using the shortcut bar as shown in Figure 2.17.
![\includegraphics[width=7mm]{img/warning_64.png}](images/img-0004.png)
If the Proving Perspective is not available in the menu, select Other...
Proving. This will open a new window which shows all available perspectives.
We should now see the window in Figure 2.18.
![\includegraphics[width=1.0\textwidth ]{img/tutorial/tut_08_proving_perspective.png}](images/img-0335.png)
The Proving Perspective contains three new important views:
- Proof Tree View (3.1.7.2)
Here we see a tree of the proof that we have done so far and the current position in it. By clicking in the tree, we can navigate within the proof. We have not yet started the proof, so there is nothing to see yet.
- Proof Control View (3.1.7.4)
This is where we perform interactive proofs.
- Goal View (3.1.7.3)
This window shows what needs to be proved at the current position inside the proof tree.
Expand the Celebrity_1 machine in the Event-B Explorer. Then expand the Proof Obligations section. We can see that the auto prover (3.1.7.5) did quite a good job. Only three proofs have not been completed1 (a completed proof is indicated by a green mark
![\includegraphics[height=2ex]{img/icons/rodin/discharged.png}](images/img-0044.png) ).
).
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Each proof has a label, e.g. remove_1/inv2/INV. Proof labels are explained in Section 3.2.7.
Let’s start with the proof remove_1/inv2/INV of Celebrity_1. To do this, double click on the proof obligation remove_1/inv2/INV. We should now see the window as shown in Figure 2.19.
![\includegraphics[width=1.0\textwidth ]{img/tutorial/tut_08_proof2.png}](images/img-0336.png)
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Make sure that you understand the different buttons in the Proof Control View (3.1.7.4).
Here we need to prove that the event remove_1 preserves the invariant inv2, 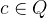 . The event’s action assigns the new value
. The event’s action assigns the new value 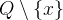 to
to 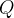 . Because we know that invariant
. Because we know that invariant 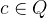 was valid before the assignment, it is sufficient to prove that we do not remove
was valid before the assignment, it is sufficient to prove that we do not remove  from
from 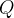 , i.e.
, i.e. 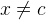 . Type this into the Proof Control View (3.1.7.4) and press the
. Type this into the Proof Control View (3.1.7.4) and press the
![\includegraphics[height=2ex]{img/icons/rodin/ah_prover.png}](images/img-0340.png) button.
button.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
In order to undo a step, click on a node in the Proof Tree View and click on the
button in the Proof Control View or open the context menu of a node and select Prune.
Take a look at the Proof Tree View. The root node should now be labelled with ah (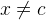 ), which is the hypothesis that we just added. This node has three children: The first proves that
), which is the hypothesis that we just added. This node has three children: The first proves that 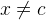 is well-defined2, which is
is well-defined2, which is 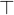 and has already been trivially proven. The second is the proof of the hypotheses
and has already been trivially proven. The second is the proof of the hypotheses 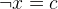 . The third is the proof of the original goal where the new hypotheses can be used.
. The third is the proof of the original goal where the new hypotheses can be used.
The new goal is 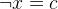 . Now, try selecting the right hypotheses by yourself in order to complete the proof (Hint: What axiom states that the celebrity does not know anybody?). To do this, click on the
. Now, try selecting the right hypotheses by yourself in order to complete the proof (Hint: What axiom states that the celebrity does not know anybody?). To do this, click on the
![\includegraphics[height=2ex]{img/icons/rodin/sh_prover.png}](images/img-0345.png) button in the Proof Control View. On the left side we should see now the Search Hypotheses view (see Figure 2.20). If you cannot find the right hypotheses, you may also just select all hypotheses. To add the selected hypothesis to the Selected Hypotheses View just click on the
button in the Proof Control View. On the left side we should see now the Search Hypotheses view (see Figure 2.20). If you cannot find the right hypotheses, you may also just select all hypotheses. To add the selected hypothesis to the Selected Hypotheses View just click on the
![\includegraphics[height=2ex]{img/icons/rodin/add.png}](images/img-0346.png) button.
button.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
There is usually no harm in selecting all hypothesis, but this approach is not optimal. By providing only necessary hypotheses and no more, we drastically increase the chance that the prover will find the solution before timing out. On large models it is next to impossible to prove everything without hand-picking the hypotheses.
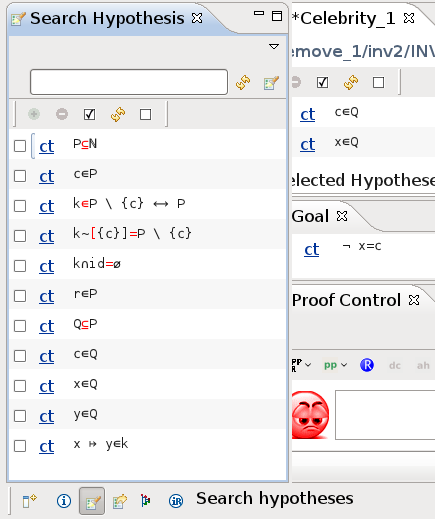
The correct hypothesis for this proof was 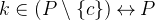 (axiom 3 from the first context). If you were unable to figure this out, add this hypothesis to the selected hypothesis window now. Now click on the
(axiom 3 from the first context). If you were unable to figure this out, add this hypothesis to the selected hypothesis window now. Now click on the
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) button to prove the goal
button to prove the goal 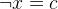 with the Predicate prover on selected hypothesis. The goal should be discharged and in the Proof Tree you should see that the first two children of the root node are proven. The Proof Control View should now show the original goal
with the Predicate prover on selected hypothesis. The goal should be discharged and in the Proof Tree you should see that the first two children of the root node are proven. The Proof Control View should now show the original goal 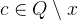 and
and 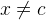 is now one of our hypotheses.3 Click a second time on the
is now one of our hypotheses.3 Click a second time on the
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) button in order to finalize the proof. The smiley in the Proof Control View should now become green indicating that all sequents of the proof tree are discharged as shown in Figure 2.21.
button in order to finalize the proof. The smiley in the Proof Control View should now become green indicating that all sequents of the proof tree are discharged as shown in Figure 2.21.
![\includegraphics[width=1.0\textwidth ]{img/tutorial/tut_08_proof_final.png}](images/img-0351.png)
After saving the proof, the proof obligation remove_1/inv2/INV in the Event-B Explorer should now have a
![\includegraphics[height=2ex]{img/icons/rodin/discharged.png}](images/img-0044.png) next to it.
next to it.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Those proof obligations that were automatically discharged are marked with a tiny “A” next to the
. As the one we just discharged was proven manually, this is now the first discharged PO without an “A”.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
There are alternative ways to prove the proof obligation. For instance, we can use the
button to load all hidden hypotheses that contain identifiers in common with the goal into the Selected Hypotheses View, and we can also use it with the selected hypotheses.
In order to move to the next undischarged proof obligation, you may also use the Next Undischarged PO button (
![\includegraphics[height=2ex]{img/icons/rodin/next_prover.png}](images/img-0353.png) ) of the Proof Control View (3.1.7.4). The next proof can be solved the same way as the last one.
) of the Proof Control View (3.1.7.4). The next proof can be solved the same way as the last one.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
As an exercise, try to prove Celebrity_2. A small hint: To do this, we have to fill in an existential quantifier. We need to instantiate b’ correctly. The auto prover should have proved that
, so look for a variable that is already in P and add this value to the Selected Hypotheses View. To instantiate b’, type the name of the variable you have chosen into the yellow box that is shown in the Goal View (3.1.7.3) and then click on the red existential quantifier. Now all open branches of the proof tree can be proved with the
prover. After this, we have completed all the proofs, and the model is ready for use.
Footnotes
- Interestingly enough, this number can vary: Provers can be configured in the preferences and changes there can have an impact on the ability to automatically discharge proofs. In addition, all provers have timeouts. On a slow machine, some proof obligations may not be discharged whereas on a faster machine with the same timeout they would be discharged.
- You may wonder how we know that this is the well-definedness proof obligation
- The prover has rewritten this as