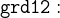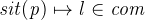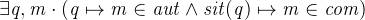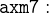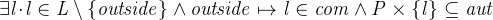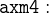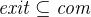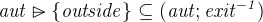Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.10.2 Deadlock Freeness of First Refinement
Now we are going to explain the main complexity of our model: the deadlock freeness proof for the first refinement.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Please remember that post-tactics should still be disabled before starting this part of the tutorial.
The difference between the first refinement and the initial model is that a new constant com has been added in order to describe which rooms are connected. Additionally, we have a constant exit, which allows anybody to get outside. Please consult the Event-B book (1.2.1) for the details regarding this model.
The event INITIALISATION does not change, but the event PASS is refined as a consequence. We assume that a person can move to another location 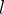 if they have the authorisation to be in
if they have the authorisation to be in 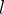 (already defined in the abstraction) and also if the location
(already defined in the abstraction) and also if the location 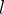 is connected to the location
is connected to the location 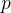 where the person is at this precise moment (represented by
where the person is at this precise moment (represented by 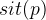 ).
).
As in the last section (2.10.1), open the door_1 machine and add a derived invariant (theorem) called DLF as follows1:
Save the file. Once again, the prover fails to prove this theorem automatically. What we want to prove is that “at least one person authorized to be in a location must also be authorized to go in another location which communicates with the first one”.
Switch over to the proving perspective and double click on DLF/THM to begin proving. When getting started, it is often a good idea to subdivide a proof into cases. In this case, one distinction of cases should be to determine whether the person is outside or not.
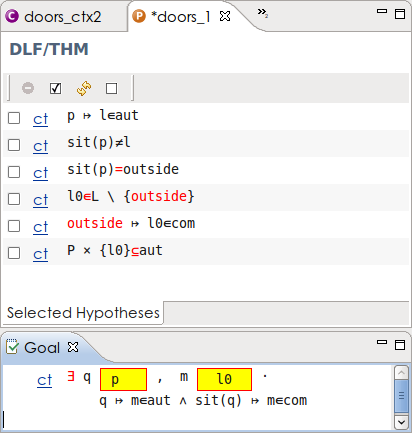
First we need a variable denoting a location in order to distinguish between the two cases. We use the deadlock freeness invariant from the initial model for this purpose. Search through the possible hypotheses and add this theorem to the selected hypotheses (Figure 2.28).
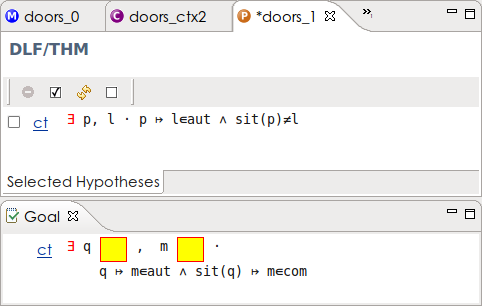
Now click on the red  to instantiate the variables p and l. This will allow us to make the case distinction. To do this, we enter the following in the Proof Control View:
to instantiate the variables p and l. This will allow us to make the case distinction. To do this, we enter the following in the Proof Control View:
![\[ sit(p) = outside \]](images/img-0407.png) |
Now press the
![\includegraphics[height=2ex]{img/icons/rodin/dc_prover.png}](images/img-0386.png) button. This will create three new nodes in the proof tree: The first one is once again the well-definedness condition, followed by the two cases that we have just defined. As always, use the
button. This will create three new nodes in the proof tree: The first one is once again the well-definedness condition, followed by the two cases that we have just defined. As always, use the
![\includegraphics[height=2ex]{img/icons/rodin/auto_prover.png}](images/img-0376.png) button to verify the well-definedness condition.
button to verify the well-definedness condition.
The first case is dealing with 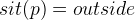 . To verify this case, we need to use axm7, which states that at least one authorized room is connected to the outside:
. To verify this case, we need to use axm7, which states that at least one authorized room is connected to the outside:
Add axm7 to the list of hypotheses. We would like to work with an instance of a location, so we instantiate this hypothesis by clicking on its red  symbol.
symbol.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Note that Rodin instantiated the variable with the name
instead of
because the name
already exists from the previous instantiation.
Now we have variables to instantiate our goal as well. We enter the value 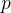 in the yellow box for q and
in the yellow box for q and 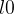 in the yellow box for m (see Figure 2.29) and press the red
in the yellow box for m (see Figure 2.29) and press the red  .
.
 and
and 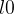 .
.This results in two new nodes to the proof tree, the first one being the well-defined proof obligation. The last remaining proof obligation can be solved with the given hypotheses. Clicking
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) will discharge both of these proof obligations.
will discharge both of these proof obligations.
Now the first case is resolved. Now let’s consider the second case, 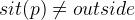 . We would like to instantiate the quantifier again, but this time we have to use different values. We still have p to substitute for q, but for the location we use the exit relationship: Our axioms tell us that there is always an exit from every location, so
. We would like to instantiate the quantifier again, but this time we have to use different values. We still have p to substitute for q, but for the location we use the exit relationship: Our axioms tell us that there is always an exit from every location, so 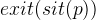 should be a valid substitution for m. Let’s perform the substitution. This advances our proof tree with a new node (and the well-definedness proof obligation, which we discharge with one click).
should be a valid substitution for m. Let’s perform the substitution. This advances our proof tree with a new node (and the well-definedness proof obligation, which we discharge with one click).
The resulting proof obligation is a conjunction. We can discharge the two parts of it by clicking on the red  symbol in the goal view. This results in two simpler goals in the proof tree. We start with the second goal.
symbol in the goal view. This results in two simpler goals in the proof tree. We start with the second goal.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
We start with the second goal instead of the first goal because doing so will provide us with hypotheses that will be beneficial in discharging the first goal. How do we know this? By experience and by playing with the proofs for a long time. Depressingly, there is no easy rule to guide us through the proving process. There are just general guidelines and experience.
The goal we start with is:
![\[ sit(p) \mapsto exit(sit(p)) \in com \]](images/img-0415.png) |
None the hypotheses that we have added so far contain 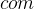 , so add axm4 to the selected hypotheses:
, so add axm4 to the selected hypotheses:
Hit the
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) button, and Rodin discharges the goal.
button, and Rodin discharges the goal.
Now deal with the last undischarged goal:
![\[ p \mapsto exit(sit(p)) \in aut \]](images/img-0418.png) |
This statement means that the person is authorized to follow the exit. To discharge this proof obligation we need to use axm6, which essentially states that “Everybody has the permission to leave from wherever they are”:
Remove the inclusion by clicking on the red  , which results in a hypothesis with universal quantifier. Instantiate this with the variables that we already have on hand. Instantiate x with p and x0 with sit(p). Examine this formula and try to understand what it means.
, which results in a hypothesis with universal quantifier. Instantiate this with the variables that we already have on hand. Instantiate x with p and x0 with sit(p). Examine this formula and try to understand what it means.
This results in two more goals in our proof tree. The first goal is the well-definedness condition which we discharge with the
![\includegraphics[height=2ex]{img/icons/rodin/auto_prover.png}](images/img-0376.png) button.
button.
The remaining goal is simple and essentially states that following the current position along the exit route will lead to a location where the user is authorized:
![\[ p \subseteq exit(sit(p)) \in aut \]](images/img-0422.png) |
We cannot discharge this with the
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) prover; However, using the
prover; However, using the
![\includegraphics[height=2ex]{img/icons/rodin/p1.png}](images/img-0387.png) prover will discharge it. Using
prover will discharge it. Using
![\includegraphics[height=2ex]{img/icons/rodin/p1.png}](images/img-0387.png) is the same as selecting related hypotheses with
is the same as selecting related hypotheses with
![\includegraphics[height=2ex]{img/icons/rodin/lasoo_prover.png}](images/img-0352.png) and then using
and then using
![\includegraphics[height=2ex]{img/icons/rodin/p0.png}](images/img-0349.png) . The danger of this approach is that if too many hypotheses are added, the prover may not be able to find a solution before timing out. In this case, it worked.
. The danger of this approach is that if too many hypotheses are added, the prover may not be able to find a solution before timing out. In this case, it worked.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
As an exercise, try to manually identify the hypotheses that were required to discharge this goal.
This concludes this section of the tutorial. Be aware that we have just looked at one small aspect of a rather sophisticated model. Also, please be aware that this tutorial gave you only an introduction to proving. To become an expert, we encourage you to study interesting models and to practice.
Footnotes
- In the future, it might be worthwhile to change this theorem to take care of a couple of issues. It only states that at least one person can move, and it may be better to state that every person can move. Furthermore, this statement is unable to detect live locks: A situation where the system oscillates between a small number of states.
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)