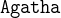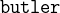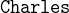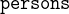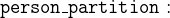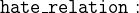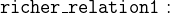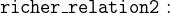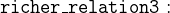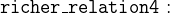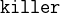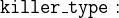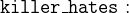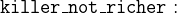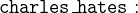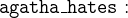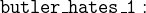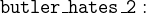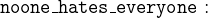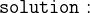Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.6.2 Populate the Context
In this section we model the Agatha puzzle step by step.
2.6.2.1 Modelling the Persons
We have three persons in the Agatha puzzle: Agatha herself, the butler and Charles. We model the three persons as constants (one constant for each person) in the corresponding CONSTANTS section:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- CONSTANTS
These constants or persons respectively are part of a set:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- SETS
Now the constants themselves are not very useful since they have no type (after creating the constants, they will be highlighted in red, which indicates a problem). The semantics of the sets (3.3.4) and constants (3.2.3.3) are specified in the axioms (3.2.3.3). As already mentioned above the persons are part of the set persons. We model this by creating a partition (3.3.4.7) in the AXIOMS section:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
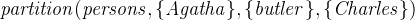
![\includegraphics[width=7mm]{img/warning_64.png}](images/img-0004.png)
Please note the curly braces {} around the constants. It’s very easy to forget these, but if they are missing, typing errors are created which are very hard to interpret for a novice.
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
The New Enumerated Set Wizard (3.1.6.2) allows you to create the constants, the set and the axiom automatically at the same time. To access this wizard, click on the New Enumerated Set Wizard tool bar item or find it under Event-B
New Enumerated Set Wizard. This will bring up a wizard into which we can enter the name of the set and the constants in the corresponding text fields. The wizard will create the enumerated set, the constants and the axiom automatically.
2.6.2.2 Modelling the Relations “Persons who hate each other” and “Who’s how rich”
We create two more constants hates and richer to model the relations “Persons who hate each other” and “Who’s how rich”. The relations are abstract, which means that they say nothing about the concrete persons (Agatha, the butler and Charles). We define the concrete relationships between the persons later in this section.
The first constant hates is an arbitrary relation (3.3.5) between persons:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
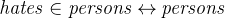
The second constant richer is also a relation between persons:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
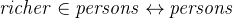
However, we know that the relation is irreflexive (no person is richer than itself):
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS

In addition, we know that the relation is transitive:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
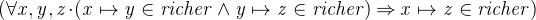
Finally, the relation is trichotomous (one person is always richer than the other or vice versa, never both directions):
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
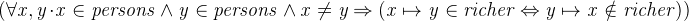
2.6.2.3 Modelling the “Crime”
Since the objective of the puzzle is to find the killer, we have to create a new constant killer which is an element of persons:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- CONSTANTS
- AXIOMS
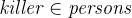
In addition, the puzzle has some more relationships between the different persons which are all modelled as axioms. We know that the killer hates his victim and is no richer than his victim:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
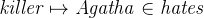
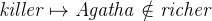
Charles hates no one that Agatha hates and Agatha hates everybody except the butler:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
![$\it hates[\{ Agatha\} ] \mathbin {\mkern 1mu\cap \mkern 1mu}hates[\{ Charles\} ] = \emptyset $](images/img-0189.png)
![$\it hates[\{ Agatha\} ] = persons \setminus \{ butler\} $](images/img-0191.png)
The butler hates everyone not richer than aunt Agatha and the butler hates everyone whom Agatha hates. However, no one hates everyone:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
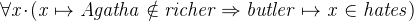
![$\it hates[\{ Agatha\} ] \subseteq hates[\{ butler\} ] $](images/img-0195.png)
![$\it \forall x \mathord {\mkern 1mu\cdot \mkern 1mu}x \in persons \mathbin \Rightarrow hates[\{ x\} ] \neq persons $](images/img-0197.png)
Finally, we have to model the solution:
![\includegraphics[width=7mm]{img/pencil_64.png}](images/img-0005.png)
- AXIOMS
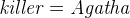
All axioms are set to “not theorem” when they are created. But we need the solution to be a theorem so that we can prove that it is valid. In order to do this, click on not theorem shown to the right of the axiom solution. This box will automatically change to theorem, and you will have set the axiom as a theorem as shown in Figure 2.12.
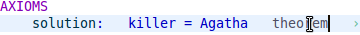
![\includegraphics[width=7mm]{img/info_64.png}](images/img-0003.png)
Theorems describe properties that are expected to be able to be derived from the axioms. Therefore, to prove a theorem you only use axioms and theorems that have already been proven.
The introduced theorem still has to be proven. Thus Rodin generates a proof obligation called solution/THM. However, at this point of the tutorial we do not want to go into more detail about proving yet.
You can use ProB to animate contexts, too. Just right-click on the context in the explorer and select Start Animation / Model Checking. If ProB finds solutions for the specified constants that fulfil the axioms, an event “SETUP_CONTEXT” is enabled that assigns values to the constants. In our example, ProB should find a solution where Agatha is the murderer. You can actually inspect the axioms and the theorem in the state view to see why they are fulfilled.
This contribution requires the ProB plugin. The content is maintained by the plugin contributors and may be out of date.
This concludes the tutorial about contexts. The following section shows the complete Context.