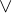Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
2.5.1 Predicates
In the traffic light example, we have already encountered several predicates: The invariants of a model and the guards of an event. The proof obligations generated by Rodin are also predicates. A predicate is simply an expression, the value of which is either true or false.
The simplest predicates are 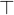 (ASCII: true) and
(ASCII: true) and 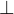 (ASCII: false). We can also assert if arbitrary objects of the same type are equal with
(ASCII: false). We can also assert if arbitrary objects of the same type are equal with  or not equal with
or not equal with 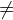 (ASCII: /=). Predicates can be combined with the usual logical operators:
(ASCII: /=). Predicates can be combined with the usual logical operators:
symbol |
ASCII |
|
conjunction (and) |
|
& |
disjunction (or) |
|
or |
implication |
|
=> |
equivalence |
|
<=> |
negation (not) |
|
not |
We can use universal quantification to express a statement that is valid for all possible values a variable might have. The universal quantifier is 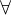 (ASCII: !). For example, in order to show that any given number
(ASCII: !). For example, in order to show that any given number 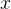 greater than zero and multiplied with two is greater than one, we can use the following expression:
greater than zero and multiplied with two is greater than one, we can use the following expression:
![\[ \forall x \mathord {\mkern 1mu\cdot \mkern 1mu}x>0 \mathbin \Rightarrow 2\cdot x > 1 \qquad \quad \textrm{ASCII: } \texttt{!x.\ x>0\ =>\ 2*x\ >\ 1} \]](images/img-0070.png) |
When a variable is introduced by a quantifier, the type of the variable must be clear. In this case Rodin can infer that 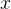 must be of type integer because the operator
must be of type integer because the operator 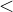 is defined only on integers. Sometimes the type cannot be inferred, e.g., in
is defined only on integers. Sometimes the type cannot be inferred, e.g., in
![\[ \forall a,b \mathord {\mkern 1mu\cdot \mkern 1mu}a\neq b \mathbin \Rightarrow b\neq a \qquad \quad \textrm{ASCII: } \texttt{!a,b.\ a/=b\ =>\ b/=a} \]](images/img-0072.png) |
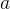 and
and 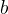 could be integers, Boolean values or some other type. In this case, we must make the type of the variables explicit by stating that
could be integers, Boolean values or some other type. In this case, we must make the type of the variables explicit by stating that 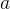 and
and 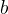 are elements of the appropriate sets. Let’s use integers again to correct the previous expression:
are elements of the appropriate sets. Let’s use integers again to correct the previous expression:
![\[ \forall a,b \mathord {\mkern 1mu\cdot \mkern 1mu}a\in \mathord {\mathbb Z}\land b\in \mathord {\mathbb Z}\land a\neq b \mathbin \Rightarrow b\neq a \]](images/img-0075.png) |
![\[ \textrm{ASCII: } \texttt{!a,b.\ a:INT \& b:INT \& a/=b => b/=a} \]](images/img-0076.png) |
The conjunction operator (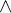 ) has a stronger binding that the implication
) has a stronger binding that the implication 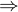 , so the above expression is equivalent to
, so the above expression is equivalent to
![\[ \forall a,b \mathord {\mkern 1mu\cdot \mkern 1mu}(a\in \mathord {\mathbb Z}\land b\in \mathord {\mathbb Z}\land a\neq b) \mathbin \Rightarrow b\neq a \]](images/img-0077.png) |
![\includegraphics[width=7mm]{img/warning_64.png}](images/img-0004.png)
If you are unsure which of the operators bind stronger, we advise you to use parenthesis to avoid mistakes.
Existential quantification on the other hand is used to state that there is an object of a certain type fulfilling a given property. The existential quantifier is  (ASCII: #). The following example expression states that there is a Boolean value different from
(ASCII: #). The following example expression states that there is a Boolean value different from 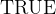 :
:
![\[ \exists x \mathord {\mkern 1mu\cdot \mkern 1mu}x\in \mathord {\mathrm{BOOL}}\land x\neq \mathord {\mathrm{TRUE}}\qquad \quad \textrm{ASCII: } \texttt{\# x.\ x:BOOL\ \& \ x/=TRUE} \]](images/img-0080.png) |
As you can see, we again added type information for 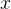 . We put the type information on the left side of the implication (
. We put the type information on the left side of the implication ( ) for the universal quantification , but for existential quantification we add it via a conjunction (
) for the universal quantification , but for existential quantification we add it via a conjunction ( ).
).